Trennung der Erfolgsquellen: Ermittlung von Konditionenbeiträgen und Transformationsbeiträgen auf Einzelgeschäftsebene

1. Einleitung

Banken müssen ihre Erfolgsquellen voneinander abgrenzen und quantifizieren können. Die Ausfüllhinweise der Bundesbank und der BaFin zum LSI-Stresstests bzw. zur Niedrigzinsumfrage (NZU) enthalten hierzu ein vereinfachtes Berechnungsschema, welches die Ableitung von Konditionenbeitrag sowie Beiträgen aus Zins- und Liquiditätsfristentransformation, aus Bonitätstransformation und aus Eigenkapitalanlage anhand geeigneter Zinskurven näherungsweise auf aggregierter Ebene erlaubt.

In diesem Artikel wird die exakte Ermittlung der entsprechenden Beiträge auf Einzelpositionsebene anhand eines mit der Marktzinsmethode sowie mit der konzeptionellen Grundlage der Aufsicht konsistenten Berechnungsschemas erläutert. Konsistenz mit der Marktzinsmethode bedeutet hier, dass alle Erfolgsbeiträge über strukturkongruente Opportunitätsgeschäfte an den Geld- und Kapitalmärkten abgeleitet werden. Hierbei werden auch die folgenden Erschwernisse adressiert:

1. Wie ist mit amortisierenden oder kapitalisierenden Strukturen wie Raten- oder Annuitätendarlehen und Spareinlagen umzugehen? Das vereinfachte Schema aus den Ausfüllhinweisen kann diese Produkte offenbar nur anhand ihrer mittleren Durchschnittslaufzeit berücksichtigen.
2. Wie können variabel verzinsliche Bankprodukte und Swaps konsistent mit der Marktzinsmethode einbezogen werden? Wie sind in diesem Zusammenhang Basis-Spreads mittels entsprechender Forward-Kurven einzubeziehen?
3. Welche zusätzlichen Anforderungen ergeben sich in Verbindung mit eingebetteten Optionen?
4. Inwieweit sollten Kaufkurse und -renditen bei börsennotierten Anleihen einbezogen werden?

Am Ende steht ein einheitliches Berechnungsschema, welches auf alle obengenannten Produkte generisch anwendbar ist.

2. Fachlicher Hintergrund und Zielsetzung

Als fachliches Fundament wird hier kurz auf den Nutzen einer Abgrenzung der Erfolgsquellen und auf die zugrundeliegenden Fragestellungen eingegangen. Zwei unterschiedliche Perspektiven sollen dabei hervorgehoben werden - die jeweils eingenommene Perspektive hat wesentliche Bedeutung für die Ausgestaltung und Parametrisierung des Berechnungsschemas:

1. Aufspaltung des Zinsergebnisses aus Risikosicht: Die Fragestellung lautet, welche Risiken aus Zins- und Liquiditätsfristentransformation und aus Bonitätstransformation den Erträgen und Aufwänden aktuell gegenüberstehen. Konkret ausgedrückt: Wenn das Institut diese Risiken zum jetzigen Zeitpunkt mit strukturkongruenten Geschäften zu aktuellen Konditionen an den Geld- und Kapitalmärkten glattstellen würde - wie sähe dann das Zinsergebnis aus? Wie ändert sich das Zinsergebnis, wenn nur einzelne dieser Risikoarten eliminiert werden? Dies ist offenbar die Perspektive der Aufsicht im LSI-Stresstest, denn es werden im Berechnungsschema aktuelle Zinskurven und aktuelle Restlaufzeiten der Geschäfte verwendet.
2. Zuordnung des Zinsergebnisses auf beteiligte Profitcenter: Eine unterschiedliche Fragestellung kann verfolgt werden, wenn die Konditionen an den Geld- und Kapitalmärkten zum Abschlusszeitpunkt jedes einzelnen Geschäfts zugrundegelegt werden. Wie sähe die Ertragssituation aus, wenn die Bank bereits zum Abschlusszeitpunkt strukturkongruent refinanziert bzw. Risiken glattgestellt hätte? Diese Sichtweise ist sinnvoll, wenn der Beitrag unterschiedlicher Profitcenter des Instituts zum Erfolg eines Geschäfts untersucht werden soll. In erster Linie geht es dabei um die Beiträge der Marktbereiche und des Treasury. Gerade in komplexeren Instituten ist darüber hinaus die Zuordnung des Treasury-Ergebnisses zu einzelnen Profitcentern innerhalb des Treasury und einzelnen Risikoarten von Relevanz.

Anmerkung: In der Vorkalkulation sowie innerhalb des Themenkomplexes FTP (Funds Transfer Pricing) entspricht der Abschlusszeitpunkt dem jetzigen Zeitpunkt. Hier können für das zu bepreisende Geschäft beide Fragestellungen, die risikobezogene Zusammensetzung der Kondition sowie die Zuordnung auf beteiligte Profitcenter, gleichzeitig adressiert werden.

Das aufsichtliche Berechnungsschema kann die letztere Fragestellung nicht adressieren, da es erstens keine Ermittlung auf Einzelgeschäftsebene vorsieht und zweitens für das Gesamtgeschäft aktuelle Marktkonditionen zugrundelegt. Beispielsweise wäre der Konditionenbeitrag eines in der Hochzinsphase abgeschlossenen Darlehens an aktuellen Zinskurven in der Niedrigzinsphase per heute gemessen sehr hoch, selbst wenn das Geschäft damals zu marktnahen Konditionen abgeschlossen wurde. Der mit aktuellen Zinskurven ermittelte Konditionenbeitrag hat inhaltlich nicht mehr viel mit dem Vertriebserfolg zum Abschlusszeitpunkt zu tun. Aus diesem Grund ist die Bezeichnung "Konditionenbeitrag" auch nicht ganz treffend für das, was übrig bleibt, wenn man vom Zinsergebnis die verschiedenen Risikobeiträge abzieht. Im vorliegenden Fall handelt es sich eher um einen Beitrag aus ursprünglich marktkonform eingepreisten, aber nicht schlagend gewordenen Risiken.

In dem hier vorgestellten Berechnungsschema können beide Fragestellungen gleichermaßen adressiert werden, je nachdem welche Berechnungsstichtage und Marktparameter je Einzelgeschäft verwendet werden.

3. Erfolgsbeiträge und Zinskurven zur Ermittlung

Wir geben zunächst die Definition der Erfolgsbeiträge aus den ausflichtlichen Ausfüllhinweisen wieder:

1. Beitrag aus Eigenkapitalanlage: Summe der ersparten Refinanzierungsaufwendungen durch das Eigenkapital
2. Beitrag der Zinsfristentransformation: Summe der Ergebnisse durch die unterschiedlichen Zinsbindungen auf der Aktiv- und Passivseite
3. Beitrag der Bonitätstransformation: Summe der Ergebnisse durch die unterschiedliche Bonitätsrisikostruktur auf der Aktiv- und Passivseite
4. Beitrag der Liquiditätstransformation: Summe der Ergebnisse durch die unterschiedlichen Kapitalbindungen auf der Aktiv- und Passivseite

Anmerkung: Der Beitrag aus Eigenkapitalanlage ist hier keineswegs zu verwechseln mit der Eigenkapitalrendite oder dem Eigenkapitalverzinsungsanspruch auf Gesamtbankebene. Es handelt sich vielmehr um den Ergebniseffekt, welcher schlicht daraus folgt, dass das Volumen der Zinsbuchaktiva sich vom Volumen der Zinsbuchpassiva unterscheidet - typischerweise ist ersteres größer - und daher selbst bei auf beiden Seiten gleicher Zinsbindung, gleicher Kapitalbindung und gleicher Bonität ein Beitrag aufgrund der unterschiedlichen Volumina entsteht. Keine konkreten Angaben macht die Aufsicht dazu, welche kalkulatorische Zins- und Kapitalbindung und welche Bonität für das Eigenkapital unterstellt werden sollen. Wir nehmen hier eine konsequente Risikosicht ein und unterstellen eine praktisch risikolose Anlage im Tagesgeld, damit sich möglichst alle Prämien für Zins-, Liquiditäts- und Bonitätsrisiken in den entsprechenden risikobezogenen Erfolgsbeiträgen wiederfinden und nicht in den Beitrag aus Eigenkapital verlagert werden. Die Eigenkapitalrendite (Return on Equity) des Zinsbuchs enthält im Gegensatz dazu alle Erfolgskomponenten auf Aktiv- und Passivseite und ist daher typischerweise deutlich höher als der Beitrag aus Eigenkapitalanlage.

Die Aufsicht skizziert in ihren Ausfüllhinweisen eine exemplarische Hierarchie von Zinskurven zur Ableitung der Erfolgsbeiträge, wobei keine eindeutigen Vorgaben zum Aufbau der Zinskurven gemacht werden. Ersichtlich ist aus dem aufsichtichen Schema aber, dass für die Ermittlung der Liquiditäts- und Bonitätstransformation jeweils vom Rating und damit vom Ausfallrisiko abhängige Kurven verwendet werden. Die Zinsfristentransformation wird in den Ausfüllhinweisen aus einer risikolosen Bewertungskurve (mit "AAA" bezeichnet") abgelesen. Wir stellen hier eine mit der aufsichtlichen Vorgabe konsistente Zinskurvenhierarchie dar:

1. Risikolose Zinskurve: Diese Zinskurve entspricht einer Geldanlage zum risikolosen Zinssatz. Das Zinsniveau am kurzen Ende dieser Kurve bestimmt den Beitrag aus Eigenkapitalanlage. Die Steilheit der risikolosen Zinskurve induziert den Beitrag aus Zinsfristentransformation.
2. Refinanzierungskurve: Diese Zinskurve entspricht einer liquiditätswirksamen Geldaufnahme zu institutsspezifischen Konditionen und induziert den Beitrag aus Liquiditätsfristentransformation. Diese Kurve kann auch als Refinanzierungsspreadkurve über der risikolosen Kurve dargestellt werden.
3. Kreditrisikobehaftete Kurve: Diese Zinskurve entspricht einer liquiditätswirksamen und kreditrisikobehafteten Anlage zu emittenten- oder kreditnehmerspezifischen Konditionen und induziert den Beitrag aus Bonitätstransformation. Diese Kurve kann auch als Credit-Spread-Kurve über der risikolosen Kurve dargestellt werden. Von allen dargestellten Kurven ermöglicht diese Kurve im Allgemeinen die marktnaheste Bewertung eines Geschäfts.
4. Wie später im Abschnitt zu den variabel verzinslichen Produkten dargestellt, kann die Zinskurvenhierarchie sinnvoll mit der sogenannten Forward-Kurve für die Bewertung zukünftiger referenzzinsabhängiger Zahlungsströme und optional zur Ermittlung eines separaten Beitrages aus Basistransformation erweitert werden.

Im aufsichtlichen Berechnungsschema werden die verschiedenen Erfolgsbeiträge anhand von Durchschnittslaufzeiten direkt aus der Kurve abgelesen. Dies stellt eine sinnvolle Annäherung und deutliche Vereinfachung dar, wird aber den tatsächlichen Tilgungstrukturen der Geschäfte, den tatsächlichen Zinskonditionen der Geschäfte und der tatsächlichen Wölbung der Zinskurven nicht im Detail Rechnung tragen können. Hierzu ist die Marktinsmethode auf Einzelgeschäftsebene in der Lage, deren Verwendung in den folgenden Abschnitten für die Ermittlung der einzelnen Erfolgsbeiträge dargestellt wird.

4. Grundschema und festverzinsliche Produkte

Dieser Abschnitt führt das Berechnungsschema für den vergleichsweise einfachen Fall von festverzinslichen Produkten ein. Hiermit sind vor allem die folgenden Produkte abgedeckt:

• Festverzinsliche Darlehen, Spareinlagen und Termingelder
• Festverzinsliche Schuldscheine und Anleihen (wobei Abschnitt 8 zu Börsennotierung zu beachten ist)
• Feste Legs von Zinsswaps (siehe Abschnitt 8 zu Zinsswaps)

Berechnungsschema

Diese Produkte haben gemeinsam, dass ihre Ertragsstruktur durch die folgenden zwei Eigenschaften charakterisiert werden kann: Erstens eine Nominalstruktur bestehend aus Aus- und Einzahlungen zu Beginn und zum Ende der Laufzeit sowie gegebenenfalls zwischenzeitliche Tilgungs- oder Ansparzahlungen. Zweitens eine Zinskonditionsstruktur (Produktzins) mit Tageszählkonvention und (möglicherweise zeitlich gestaffelter) Rate. Aus dieser ergibt sich durch Verzinsung des sich jeweils aus der Nominalstruktur ergebenden ausstehenden Betrages ein feststehender Zinscashflow.

Im Geiste der Marktzinsmethode lässt sich für diese Geschäfte unter Verwendung einer beliebigen Zinsstruktur leicht ein Einstandszinssatz, d.h. eine faire Rate, ermitteln. Die faire Rate ist derjenige Zinssatz, zu dem am von der Zinsstruktur repräsentierten Markt ein Geschäft mit der gegebenen zukünftigen Nominalstruktur abgeschlossen oder, gleichbedeutend, ein bestehendes Geschäft glattgestellt werden könnte. Bei dieser Rate ist folglich der Barwert der zukünftigen Zins- und Tilgungszahlungen gleich dem aktuell ausstehenden Betrag. Die Berechnung geschieht anhand der folgenden drei Schritte:

• Ermittlung des Barwerts bei Nullzins: Es wird der Barwert der zukünftigen Nominal-Cashflows durch Diskontierung mit der Zinsstruktur berechnet.
• Ermittlung der Annuität: Es wird der Barwert der zukünftigen Zinscashflows - bei Annahme eines konstanten Zinssatzes von 100% - durch Diskontierung mit der Zinsstruktur berechnet.
• Ermittlung des Einstandszinssatzes: Der Einstandszinssatz berechnet sich, indem vom aktuell ausstehenden Betrag der Barwert bei Nullzins abgezogen wird und das Ergebnis durch die Annuität geteilt wird.

Die folgende Grafik illustriert die Ermittlung des Einstandszinssatzes für den Fall eines Darlehens:

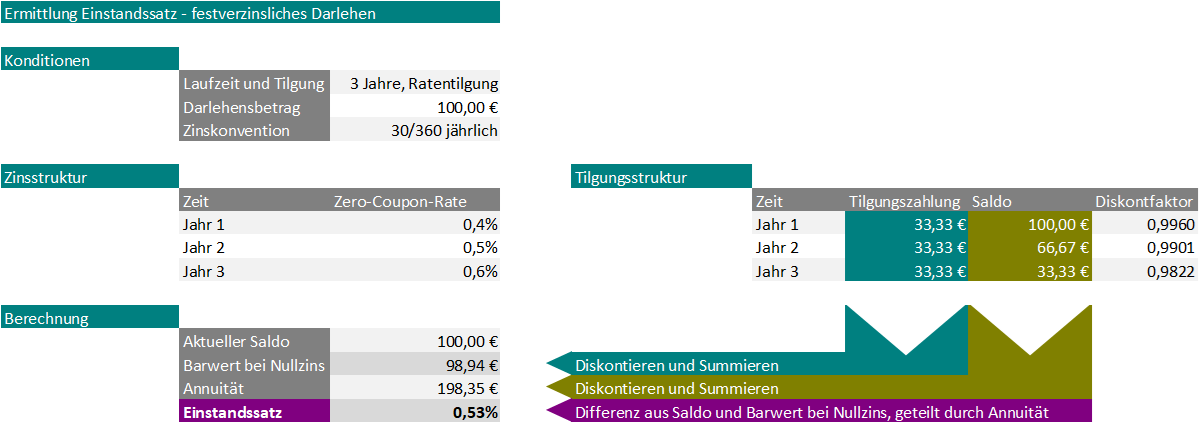
Die Berechnung ist in diesem Beispiel anhand weniger Überlegungen nachvollziehbar. Der Barwert bei Nullzins beträgt knapp 99 Euro und liegt damit ca. einen Euro unterhalb des Nominalwerts von 100 Euro. Da die Annuität etwa 200 Euro beträgt, bringt ein zusätzlicher Prozentpunkt auf der Zinskondition etwa 2 Euro im Barwert. Ein halber Prozentpunkt auf der Zinskondition sollte daher den Barwert um etwa einen Euro erhöhen und etwa auf den Nominalwert von 100 Euro bringen. Die exakte Rechnung ergibt tatsächlich einen Einstandssatz in der Nähe eines halben Prozentpunkts.

Mit diesem einfachen Werkzeug ausgestattet, lassen sich nun Einstandszinssätze gemäß der Zinskurvenhierarchie berechnen:

• Risikoloser Einstandszinssatz E1: Dies ist der faire Zinssatz einer Anlage im Tagesgeld mit den Konventionen des Ursprungsgeschäfts unter Verwendung der risikolosen Zinskurve. E1 ist nichts anderes als der Tagesgeldzins, ausgedrückt in der Konvention des Ursprungsgeschäfts.
• Zinsrisikobehafteter Einstandszinssatz E2: Dies ist der faire Zinssatz einer fristenkongruenten Refinanzierung ohne langfristige Bereitstellung oder Aufnahme von Liquidität (zur Praktikabilität einer solchen Refinanzierung verweisen wir auf den untenstehenden Abschnitt zur Parametrisierung). Hierzu wird der Einstandszinssatz des Ursprungsgeschäfts nach der obigen Berechnungsvorschrift unter Verwendung der risikolosen Zinskurve berechnet. Im Gegensatz zum Tagesgeld ist der Barwert dieser Refinanzierung aufgrund seiner langen Zinsbindung substantiell vom Zinsniveau abhängig, weshalb wir hier vom zinsrisikobehafteten Einstandszinssatz sprechen.
• Zins- und Liquiditätsrisikobehafteter Einstandszinssatz E3: Dies ist der faire Zinssatz einer liquiditätswirksamen fristenkongruenten Refinanzierung, d.h. eine Refinanzierung zu institutsspezifischen Konditionen. Hierzu wird der Einstandszinssatz des Ursprungsgeschäfts unter Verwendung der Refinanzierungskurve berechnet.
• Zins-, Liquiditäts- und Kreditrisikobehafteter Einstandszinssatz E4: Dies ist der faire Zinssatz eines liquiditätswirksamen Opportunitätsgeschäfts unter Berücksichtigung einer angemessenen Bonitätsprämie. Hierzu wird der Einstandszinssatz des Ursprungsgeschäfts unter Verwendung der kreditrisikobehafteten Kurve berechnet.

Der Konditionenbeitrag kann nun als Differenz zwischen dem aktuellen Produktzins und E4 berechnet werden. Die Differenzen zwischen den errechneten Einstandszinssätzen ergeben die entsprechenden Erfolgsbeiträge. Der Einstandszinssatz E1 entspricht schliesslich dem Beitrag aus Eigenkapitalanlage.

In der folgenden Abbildung ist das Grundschema für Festzinsprodukte dargestellt, welches wir um weitere Produkte erweitern werden.

Anmerkung: Das dargestellte Berechnungschema zielt auf die Ermittlung der prozentualen Ertragsbestandteile zum Betrachtungszeitpunkt ab. So geht für die Bestimmung des Konditionenbeitrags nur der aktuelle Produktzins ein, zukünftige Staffelungen bleiben zunächst außen vor. Sollen das Zinsergebnis und seine Erfolgskomponenten auf Perioden nach dem Betrachtungszeitpunkt abgegrenzt werden, z.B. im Rahmen einer NII-Simulation (Net Interest Income), ist der jeweils für die entsprechende Periode gültige Produktzins anzuwenden.

Parametrisierung

Risikolose Zinskurve

Zur Wahl der risikolosen Zinskurve: Wenn das Berechnungsschema eine Abgrenzung der Erträge aus Zinsfristentransformation von den Erträgen aus Liquiditäts- und Bonitätstransformation leisten soll, muss die risikolose Zinskurve solche Geschäfte repräsentieren, deren Abschluss möglichst keine Auswirkung auf das gemessene Liquiditätsrisiko und das gemessene Kreditrisiko, wohl aber auf das gemessene Zinsrisiko hat.

Aus Sicht des Autors wird dieser Anforderung eine OIS-Kurve, d.h. eine aus Overnight-Geschäften und Swaps gegen den Overnight-Zinssatz konstruierte Kurve, am ehesten gerecht. Eine endfällige Geldanlage zu den Konditionen der OIS-Kurve zu einer gegebenen Fristigkeit entspricht einer rollierenden Anlage des Nominalbetrages im Tagesgeld und dem gleichzeitigen Abschluss eines OIS-Swaps mit der gegebenen Fristigkeit. Auch eine Refinanzierung eines Produktes mit Tilgungsstruktur zu den in der OIS-Kurve implizierten Konditionen könnte praktisch durch rollierende Anlage im Tagesgeld und Festschreiben der zukünftigen Zinskonditionen über OIS-Swaps erfolgen, auch wenn ein solches Vorgehen auf Einzelgeschäftsebene wohl kaum der gängigen Praxis entspricht. Ein Verlust des Nominalbetrags in Folge von Kreditereignissen ist bei einer solchen Anlage aufgrund der kurzen Kapitalbindung und der für Swaps bestehenden Kreditrisikominderungstechniken praktisch ausgeschlossen. Die Anlage kann aus diesem Blickwinkel als kreditrisikolos gelten. Eine nennenswerte Liquiditätswirkung haben diese Geschäfte auch nicht, da keine fristenkongruente Geldanlage oder Geldaufnahme in Höhe des Nominalbetrags erfolgt, sondern nur Liquiditätswirkungen zweiter Ordnung aus dem Margining der Derivate entstehen. Aus diesen Gründen sind OIS-Kurven für die Separierung der Erträge aus Zinsfristentransformation von denen aus Liquiditäts- und Bonitätstransformation gut geeignet.

Als Alternative zur OIS-Kurve erscheint auch die Verwendung von Swap-Kurven auf Basis des währungsspezifischen Standard-Swapmarktes (z.B. eine Sechs-Monats-Euribor-Swapkurve im Euroraum) plausibel, da viele Banken in diesem Markt aktiver sind als im Markt der OIS-Swaps, und die obengenannten Argumente näherungsweise auch hier gültig sind.

Risikobehaftete Zinskurven

Während die risikolose Zinskurve sinnvollerweise über das gesamte zinstragende Geschäft einheitlich gewählt wird, sind die Refinanzierungskurve sowie die kreditrisikobehaftete Kurve grundsätzlich geschäftsabhängig zu wählen. Hier werden beispielhafte Parametrisierungen für typische Festzinsgeschäfte dargestellt:

• Darlehen: Als Refinanzierungskurve wird hier typischerweise eine ungedeckte (d.h. aus Kursen von ungedeckten Inhaberschuldverschreibungen des Instituts abgeleitete) oder eine gedeckte (d.h. aus Kursen von Pfandbriefen oder anderen Covered Bonds abgeleitete) Kurve verwendet, je nach dem, ob das Grundgeschäft für den Deckungsstock verwendet werden kann. Als kreditrisikobehaftete Kurve kommt die Ergänzung der Refinanzierungskurve mit einer additiven Bonitätsprämie in Frage. Für die Ermittlung dieser Bonitätsprämie stehen geeignete Methoden zur Verfügung, die das Ausfallrisiko anhand von Migrationsmatrizen berücksichtigen und statistische Annahmen zur Werthaltigkeit eventuell vorhandener Sicherheiten einbeziehen können.
• Einlagen und Emissionen: Hier kann die kreditrisikobehaftete Kurve mit der Refinanzierungskurve identisch gewählt werden (keine Bonitätstransformation auf der Passivseite) und die Refinanzierungskurve reflektiert typischerweise die institutsspezifischen Refinanzierungskonditionen am Geld- und Kapitalmarkt.
• Feste Legs von geclearten oder bilateral besicherten Zinsswaps: Hier sollte die Refinanzierungskurve sowie die kreditrisikobehaftete Kurve identisch zur risikolosen Kurve gewählt werden. Damit verschwinden die Beiträge aus Liquiditätsfristen- und Bonitätstransformation. Dies wird dem Zinsswap als reinem Steuerungsinstrument für die Zinsfristentransformation gerecht und führt bei Verwendung einer OIS-Kurve als risikolose Kurve zu einer marktkonformen Bewertung.

5. Variabel verzinsliche Produkte

In diesem Abschnitt wird das obige Bewertungsschema auf variabel verzinsliche Produkte angewandt. Dies sind vor allem

• Referenzzinsgebundene Darlehen und Termingelder
• Referenzzinsgebundene Schuldscheine und Anleihen (wobei Abschnitt 7 zu Börsennotierung zu beachten ist)
• Variable Legs von Zinsswaps (siehe Abschnitt 8 zu Zinsswaps)

Nach dem Schema der Aufsicht ist für diese Produkte der Beitrag aus Zinsfristentransformation vereinfachend anhand der Zinsbindung aus der Kurvenhierarchie abzulesen. Eine Floating Rate Note mit 5 Jahren Restlaufzeit und nächstem Zinsanpassungstermin in 3 Monaten wird dort also beispielsweise nicht anders behandelt als ein Straight Bond mit 3 Monaten Restlaufzeit. Eine strukturkongruente Refinanzierung im Sinne der Marktzinsmethode wird aber durch ein bis zur Zinsbindung des Produktes laufendes Festzinsgeschäft in der Praxis kaum erreichbar sein, da mit einer kurzlaufenden Refinanzierung eine Immunisierung gegen Zinsschocks nur unter strengen, in der Praxis selten erfüllbaren Bedingungen erreicht wird: Werden zur Diskontierung und zur Ermittlung der Forwardraten unterschiedliche Kurven verwendet, oder enthält das Produkt wie üblich einen festen Spread über dem Referenzzins, unterscheiden sich Bewertung und Zinsrisiko teils deutlich zwischen Ursprungsgeschäft und kurzlaufender Refinanzierung. Im folgenden wird die Ermittlung der Erfolgsbeiträge jeweils durch eine Hierarchie hypothetischer Opportunitätsgeschäfte analog zum obigen Vorgehen für Festzinsgeschäfte erläutert.

Anders als bei festverzinslichen Produkten werden die Zinskonditionen eines referenzzinsgebundenen Geschäfts nicht durch einen Produktzins, sondern durch den Spread über dem Referenzzins bestimmt. An die Stelle des Einstandszinssatzes tritt folglich ein Einstandsspread. Dieser lässt sich - völlig analog zum Einstandszinssatz bei festverzinslichen Produkten - in drei Schritten ermitteln:

• Ermittlung des Barwerts bei Nullspread: Es wird der Barwert der zukünftigen Nominal- und Zinscashflows unter Annahme eines Spreads von null berechnet. Hierbei kommt eine Forward-Kurve zur Ermittlung der Zinscashflows und die jeweils gewählte Diskont-Kurve zum Einsatz. Die beiden Kurven müssen nicht übereinstimmen.
• Ermittlung der Annuität: Es wird der Barwert der zukünftigen Zinscashflows - bei Annahme eines konstanten festen Zinssatzes von 100% - durch Diskontierung mit der Diskont-Kurve berechnet.
• Ermittlung des Einstandsspreads: Der Einstandsspread berechnet sich, indem vom aktuellen Saldo der Barwert bei Nullspread abgezogen wird und das Ergebnis durch die Annuität geteilt wird.

Das Berechnungsschema wird nun ähnlich wie bei den Festzinsprodukten durchlaufen.

• Risikoloser Einstandszinssatz E1: Dies ist genau wie bei den Festzinsprodukten der faire Zinssatz einer Anlage im Tagesgeld mit den Konventionen des Ursprungsgeschäfts unter Verwendung der risikolosen Zinskurve.
• Zinsrisikobehafteter Einstandszinssatz E2: Dies ist analog zu den Festzinsprodukten der faire Zinssatz einer fristenkongruenten Refinanzierung ohne Liquiditätswirkung. Im Falle von variabel verzinslichen Produkten handelt es sich um eine Refinanzierung auf Basis des gleichen Referenzzinses, der auch für das Ursprungsgeschäft maßgeblich ist. Hierzu wird der Einstandsspread S2 des Ursprungsgeschäfts nach der obigen Berechnungsvorschrift unter Verwendung der risikolosen Zinskurve als Diskontkurve und der Forward-Kurve zur Projektion der zukünftigen Zinscashflows berechnet. Der Einstandszinssatz E2 ergibt sich durch Addition des Einstandsspreads S2 zum aktuellen Fixing des Referenz-Index. Der Einstandszinssatz E2 unterscheidet sich von E1 vor allem durch die enthaltene Basis, die Differenz zwischen Forward-Kurve und risikoloser Zinskurve. Aufgrund der typischerweise kurzen Zinsbindung des variablen verzinslichen Geschäfts ergibt sich aus der Steilheit der Zinskurven nur ein geringer Beitrag.
• Zins- und Liquiditätsrisikobehafteter Einstandszinssatz E3: Dies ist der faire Zinssatz einer liquiditätswirksamen fristenkongruenten Refinanzierung, d.h. eine Refinanzierung zu institutsspezifischen Konditionen. Hierzu wird der Einstandsspread S3 des Ursprungsgeschäfts unter Verwendung der Refinanzierungskurve als Diskontkurve und der Forward-Kurve zur Projektion der zukünftigen Zinscashflows berechnet. Durch Addition des aktuellen Fixings erhält man den Einstandszinssatz.
• Zins-, Liquiditäts- und Kreditrisikobehafteter Einstandszinssatz E4: Dies ist der faire Zinssatz eines liquiditätswirksamen Opportunitätsgeschäfts unter Berücksichtigung einer angemessenen Bonitätsprämie. Die Berechnung erfolg analog zu den Einstandszinssätzen E2 und E3, jedoch unter Verwendung der kreditrisikobehafteten Kurve als Diskontkurve.

Der Konditionenbeitrag kann nun als Differenz zwischen dem aktuellen Produktzins und E4 berechnet werden. Der Produktzins ist dabei das aktuelle Referenzzins-Fixing zuzüglich des aktuellen Spread. Die Erfolgsbeiträge können nun völlig analog zum Vorgehen bei Festzinsprodukten ermittelt werden.

Parametrisierung

Für die Parametrisierung gelten zunächst die gleichen Hinweise wie für Festzinsprodukte. Darüber hinaus ist die Forward-Kurve geeignet zu wählen. Eine marktkonforme Parametrisierung lässt sich erreichen, wenn eine Swap-Kurve verwendet wird, die am kurzen Ende aus einem Deposit-Satz entsprechend dem maßgeblichen Referenzzins und am langen Ende aus Swaps gegen den maßgeblichen Referenzins aufgebaut wird. Wenn möglich können zusätzliche Stützstellen zwischen dem Deposit und dem kürzesten Swap auf Basis von Forward-Rate-Agreements (FRAs) ergänzt werden.

Abgrenzung des Beitrages aus Basistransformation

Im wie oben ermittelten Einstandssatzsind E2 sind nun Risikoprämien für zwei Risikokomponenten enthalten, erstens für das Risiko einer Änderung der risikolosen Zinskurve (allgemeines Zinsrisiko) und zweitens für das Risiko der Änderung des Spreads zwischen risikoloser Zinskurve und tenorspezifischer Forwardkurve (Basisrisiko). Beide Risiken werden durch das zur Ermittlung des Einstandszinssatzes E2 verwendete hypothetische Refinanzierungsgeschäft - eine strukturkongruente Refinanzierung mit deckungsgleichem Referenzzins - glattgestellt.

Die Risikoprämien lassen sich alternativ auch als explizite Erfolgsbeiträge voneinander abgrenzen. Hierzu kann leicht ein zusätzlicher Einstandszinssatz E2B unter Verwendung der risikolosen Zinskurve sowohl zur Diskontierung als auch zur Projektion künftiger referenzzinsgebundener Cashflows errechnet werden. Dieser Einstandszinssatz entspricht einer hypothetischen Refinanzierung im Tagesgeld mit Absicherung aller zukünftigen Zinsen an demjenigen Swapmarkt, aus dem die risikolose Kurve aufgebaut wurde. Eine solche Refinanzierung eliminiert das allgemeine Zinsrisiko, aber nicht das Basisrisiko.

Folglich lässt sich der oben errechnete Beitrag aus Zinsfristentransformation in einen Beitrag aus Basistransformation E2B - E2 und einen Beitrag E2B - E1 zerlegen - letzterer kann als Beitrag aus Zinsfristentransformation im engeren Sinn bezeichnet werden. Diese Zerlegung ist dann sinnvoll, wenn Basisrisiken auch separat gesteuert werden.

6. Produkte mit eingebetteten Optionen

Auch eingebettete Optionen enthalten Risiken, denen entsprechende Ergebnisbeiträge als Risikoprämie gegenüberstehen. Da das Berechnungsschema auf der Marktzinsmethode und daher auf einer Barwertlogik beruht, lassen sich Ergebnisbeiträge aus Optionalitäten unabhängig vom verwendeten Optionspreismodell nahtlos in das Schema integrieren. Hiermit können insbesondere Ergebnisbeiträge aus Optionalitäten für folgende Produkte abgebildet werden:

• Kündigungsrechte in Verbindung mit Darlehen nach § 489 BGB
• Kündbare Spareinlagen
• Anleihen mit Kündigungsrechten zum Nennwert
• Zinsbegrenzungsvereinbarungen bei variabel verzinslichen Produkten

Für diese Produkte lässt sich jeweils ein Einstandszinssatz E5 unter Verwendung des relevanten Optionspreismodells bestimmen. Für marktnahe Bewertungsverfahren - Zinsstrukturmodelle wie Hull-White für Kündigungsrechte oder das Bachelier-Modell für Zinsbegrenzungsvereinbarungen - ist dies nicht mehr in geschlossener Form möglich wie oben dargestellt. Vielmehr ist hier eine Zielwertsuche notwendig - gesucht ist derjenige Zinssatz (oder Spread über dem Referenzzins), der unter dem jeweils verwendeten Optionspreismodell zu einer Par-Bewertung des Gesamtgeschäfts führt.

Nachdem der Einstandszinssatz E5 ermittelt ist, berechnet sich der optionspreisbereinigte Konditionenbeitrag nunmehr als Produktzins abzüglich E5 und die Optionsprämie lässt sich als E5 - E4 ermitteln.

7. Besonderheiten bei börsennotierten Anleihen

Börsennotierte Anleihen haben typischerweise eine Kursversorgung und werden im allgemeinen über oder unter Pari, d.h. mit einem Bewertungsauf- oder Abschlag, gekauft und verkauft. Der Bewertungsauf- oder Abschlag wird je nach Rechnungslegungsvorschrift auf die Restlaufzeit verteilt und geht in das Zinsergebnis ein. Folglich ist auch das Zinsergebnis von der Rechnungslegungsvorschrift abhängig.

Um diesen Anwendungsfall in das obige Berechnungsschema zu integrieren, ist eine Zusatzüberlegung erforderlich: Wie sollten die strukturkongruenten Opportunitätsgeschäfte aussehen? Denkbar ist die Modellierung der Opportunitätsgeschäfte als Bondkäufe oder -Verkäufe mit den gleichen Bewertungsauf- oder Abschlägen. Nach Auffassung des Autors sollten aber zu Pari notierende Geschäfte verwendet werden, da eine Modellierung über Käufe und Verkäufe mit Abschlag eine weitere Abhängigkeit von der Rechnungslegungsvorschrift induziert und damit die Rechnung und Interpretation verkompliziert, ökonomisch aber keinen weiteren Erkenntnisgewinn gegenüber einer Modellierung mit Par-Käufen und -Verkäufen bietet. Für die ökonomische Aussagekraft ist letzlich die Wahl der richtigen Bewertungskurve ausschlaggebend.

Ausgehend von dieser Überlegung können die Einstandszinssätze E1 bis E4 wie oben beschrieben ermittelt werden. Genau wie das Zinsergebnis selbst ist auch der Konditionenbeitrag von der Rechnungslegungsvorschrift abhängig. Soll ein Konditionenbeitrag als Prozentsatz in der Konvention des Grundgeschäfts errechnet werden, ist zunächst das Zinsergebnis in einen Prozentsatz in der Konvention des Grundgeschäfts umzurechnen und dann der Einstandszinssatz E4 abzuziehen.

Die kreditriskobehaftete Zinskurve sollte in diesem Fall idealerweise so gewählt werden, dass die Bewertung des Ursprungsgeschäfts mit der kreditrisikobehafteten Zinskurve mut der Marktbewertung zusammenfällt. Hierzu ist des sinnvoll, eine Emittenten- oder Emittentengruppenspezifische Zinskurve mit einem anleihespezifischen Z-Spread zu ergänzen: Der Z-Spread (oder auch idiosynkratische Spread) ist definiert als über die Stützstellen konstanter additiver Spread über den Zero-Coupon-Raten einer Ausgangszinskurve, sodass die Bewertung der Anleihe über die so "verschobene" Zinskurve mit der Marktbewertung zusammenfällt.

8. Zinsswaps

Wir werden im folgenden sehen, dass sich Zinsswaps als Gesamtgeschäft betrachtet mit wenigen Zusatzüberlegungen konsistent in das Berechnungsschema integrieren lassen, dass aber auch eine Abbildung der einzelnen Legs als fest- und variabelverzinsliche Bonds ohne weiteres - mit in der Gesamtsicht ökonomisch identischen Ergebnissen - möglich ist.

Abbildung des Gesamtgeschäfts

Swaps sind außerbilanzielle Geschäfte zur Steuerung der Zinsfristentransformation ohne unmittelbare Liquiditätswirkung. Wir gehen darüber hinaus von Minderung der Kontrahentenrisiken durch bilaterale Besicherung oder Clearing aus, sodaß die Beiträge aus Eigenkapitalanlage, Liquiditätsfristentransformation und Bonitätstransformation verschwinden. Der Konditionenbeitrag ist offenbar durch die Differenz aus der vereinbarten Rate auf der fixen Seite des Swaps und der aktuellen Swaprate eines strukturkongruenten Geschäfts gegeben, denn zur aktuellen Swaprate ließe sich der Swap definitionsgemäß glattstellen und die genannte Differenz bliebe als risikoloser Beitrag bestehen.

Abbildung der Legs separat

Zinsswaps lassen sich nahtlos in das Bewertungsschema integrieren, indem das festverzinsliche Leg und das variabel verzinsliche Leg jeweils separat betrachtet werden und die einzelnen Beiträge wie in den Abschnitten zu fest- und variabel verzinslichen Produkten beschrieben ermittelt werden. Zinsswaps enthalten typischerweise keinen Nominalaustausch. Damit das Berechnungsschema funktioniert, müssen die Swap-Legs analog zu Bonds mit Nominalzahlungen abgebildet werden. Die Nominalzahlungen von festem und variablem Leg gleichen sich in der Gesamtsicht aus, das "Dazuerfinden" dieser Zahlungen ist also ökonomisch angemessen.

Die Konsequenzen einer solchen Abbildung:

• Der Beitrag aus Eigenkapitalanlage verschwindet für das Gesamtgeschäft, da die monetären Beiträge des fixen und des variablen Legs identisch sind. Dies ist konsistent mit der Abbildung als Gesamtgeschäft.
• Die Beiträge aus Liquiditäts- und Bonitätsfristentransformation verschwinden, sofern die risikolose Zinskurve zur Bewertung des Geschäfts verwendet wird.
• Der Beitrag aus Zinsfristentransformation setzt sich aus den entsprechenden Beiträgen der einzelnen Geschäfte zusammen. An die Stelle eines fairen Swaps als Opportunitätsgeschäft zur Glattstellung der Fristentransformation treten also zwei Par-Bonds, jeweils ein fixer und ein variabler. Gemeinsam ergeben diese einen Swap, der auf der variablen Seite einen kleinen Spread über dem Referenzzins enthält und den Barwert null hat. Haben die beiden Legs die gleichen Zinszahlungstermine, entsprechen fixe Rate und Spread zusammengenommen wieder der Swaprate, die bei Abbildung des Gesamtgeschäfts zum Tragen kommt. Es ergibt sich also exakt der gleiche Fristentransformationsbetrag.

Haben die beiden Legs unterschiedliche Zahlungsfrequenzen, erhält man in Summe je nach Verlauf der Zinskurve einen geringfügig unterschiedlichen Fristentransformationsbeitrag im Vergleich mit der Abbildung des Gesamtgeschäfts. Da beide Opportunitätsgeschäfte aber tatsächlich zu den so ermittelten Konditionen abschließbar wären, ist die separate Abbildung der Legs nach Auffassung des Autors gleichwertig, wie im folgenden ausgeführt wird.

Die folgende Tabelle zeigt als Berechnungsbeispiel die Ergebnisse beider Abbildungen eines zehnjährigen Swaps, der auf der fixen Seite jährlich und auf der variablen Seite halbjährlich zahlt. Es wurden Marktdaten (OIS-Kurve zur Diskontierung und Sechs-Monats-Euribor-Kurve zur Ermittlung der Forward-Raten) vom 31.08.2020 verwendet.

	Fairer Swap	Zwei Par-Bonds
Nominalwert	10.000,00	10.000,00
Barwert fixes Leg	119,09	0,00
Barwert variables Leg	119,09	0,00
Barwert gesamt	0,00	0,00
Fixe Rate	-0,1259%	-0.2426%
Spread variable Seite	-0,0000%	-0,1168%
Festzinsertrag: Differenz Fixe Rate und Spread	-0,1259%	-0,1258%

Das Berechnungsbeispiel zeigt, dass sich die Ergebnisbeiträge der beiden Abbildungen - ein fairer Swap oder zwei Par-Bonds - um nur einen hundertstel Basispunkt unterscheiden. In einem anderen Marktumfeld kann der Unterschied größer sein, was zu einem scheinbaren Widerspruch führt, der hier aufgelöst werden soll: In der Ertragssicht macht es keinen Unterschied, ob ein Prozentpunkt auf der fixen Seite jährlich oder als Spread auf der variablen Seite halbjährlich gezahlt wird - die Ertragssicht ist agnostisch gegenüber Zinsfrequenzen. Für unseren Zweck ist aber der - bezüglich Zahlungsfrequenzen unbestechliche - Barwert entscheidend. Beide Opportunitätsgeschäfte, fairer Swap und Kombination aus zwei Par-Bonds, sind mit Barwert null fair, stellen das Ursprungsgeschäft glatt und sind daher zur Separierung der Zinsfristentransformation von den übrigen Ertragsquellen trotz unterschiedlichem Ergebnis in der Ertragssicht gleichermaßen geeignet.

9. Zusammenfassung und schematische Darstellung

In den vorherigen Abschnitten wurde das für Festzinsprodukte gültige Grundschema um variabel verzinsliche Produkte, Produkte mit eingebetteten Optionen sowie um Zinsswaps erweitert. Es ergibt sich folgendes Gesamtschema, welches für alle erwähnten Produkte verwendet werden kann.

Mit diesem Berechnungsschema

• ist eine Trennung der Erfolgsquellen im von der Aufsicht vorgegebenen fachlichen Rahmen auf Einzelpositionsebene ermittelbar,
• sind sowohl festverzinsliche als auch variabel verzinsliche Produkte und insbesondere Zinsswaps abbildbar (letztere auf Basis der Darstellung jedes einzlenen Legs)
• wird verschiedenen Zinszahlungsfrequenzen, amortisierenden Strukturen und falls notwendig auch optionalen Bestandteilen exakt im Sinne der Marktzinsmethode Rechnung getragen.

Anhang. Implementierung in JSON risk

Wir stellen hier eine beispielhafte Implementierung auf Basis der freien und quelloffenen Bewertungsbibliothek JSON risk dar. Weitere Informationen zu JSON risk sind auf der Dokumentationsseite sowie unter GitHub verfügbar.

Mit JSON risk ist die Anwendung eines solchen Berechnungsschemas einfach möglich, da die Ermittlung des Einstandssatz (der fairen Rate) sowie eines fairen Spreads in einer entsprechenden Hilfsfunktion fixed_income.fair_rate_or_spread gekapselt ist. Das folgende Code-Beispiel zeigt die Ermittlung der Beiträge für ein Festzinsprodukt. Zunächst muss das Produkt mit seinen Konditionen definiert werden:

// definiere das Produkt
var product_json={
    notional: 100,
    effective_date: "01.01.2010",
    maturity: "31.12.2030"
    tenor: 6,
    fixed_rate: 0.0125
    dcc: "30/360"
};
var product=new JsonRisk.fixed_income(product_json);

Zur Ermittlung des Beitrags aus Eigenkapital ist zusätzlich ein Tagesgeld-Opportunitätsgeschäft zu definieren:

// definiere das Tagesgeld-Opportunitätsgeschäft
var overnight_json={
    notional: 100,
    effective_date: $scope.params.valuation_date,
    maturity: JsonRisk.add_days(JsonRisk.get_safe_date(JsonRisk.valuation_date), 1),
    tenor: 1,
    fixed_rate: 0.0,
    calendar: "TARGET",
    bdc: "f",
    dcc: product.dcc,
    adjust_accrual_periods: true
};
var overnight=new JsonRisk.fixed_income(overnight_json);

Davon ausgehend können nun die Einstandszinssätze und Erfolgsbeiträge ermittelt werden. Hierzu werden die Variablen dc als risikolose Kurve, rc als Refinanzierungs-Spreadkurve über der risikolosen Kurve sowie sc als Bonitäts-Spreadkurve über der risikolosen Kurve als bereits definiert angenommen.

// ermittle den Beitrag aus Eigenkapitalanlage E1 auf Basis des Tagesgeldgeschäfts
var e1=overnight.fair_rate_or_spread(dc, null, null);

// ermittle die übrigen Einstandszinssätze auf Basis des tatsächlichen Geschäfts
var e2=product.fair_rate_or_spread(dc, null, null); // ohne Spread
var e3=product.fair_rate_or_spread(dc, rc, null);   // mit Refinanzierungsspread
var e4=product.fair_rate_or_spread(dc, sc, null);   // mit Bonitätsspread

// gebe die Erfolgsbeiträge als JSON aus
return {
    Eigenkapitalanlage: e1,
    Zinsfristentransformation: e2 - e1,
    Liquiditaetsfristentransformation: e3 - e2,
    Bonitaetstransformation: e4 - e3,
    Konditionenbeitrag: instrument_json.fixed_rate - e4
};

Das obige Code-Beispiel ist in einer abgewandelten Form, die auch variable Produkte unterstützt, in der Web-Anwendung JSON risk Bonds frei verfügbar. Dort können innerhalb der grafischen Benutzeroberfläche sämtliche Einstellungen wie Laufzeit, Zinskonditionen und Tilgungsstrukturen des betrachteten Geschäfts und Parametrisierungseinstellungen vorgenommen werden. Die Erfolgskomponenten werden in prozentualer Form in der Konvention des betrachteten Geschäfts ausgegeben.